Prirodni fenomeni i procesi oko nas prilično su složeni. Za njihov točan fizički opis treba koristiti glomazan matematički aparat i uzeti u obzir velik broj značajnih čimbenika. Kako bi se izbjegao ovaj problem, u fizici se koriste neki pojednostavljeni modeli koji uvelike olakšavaju matematičku analizu procesa, ali praktički ne utječu na točnost njegovog opisa. Jedan od njih je model idealnog plina. Razmotrimo to detaljnije u članku.
Koncept idealnog plina
Idealni plin je stanje agregacije tvari, koje se sastoji od materijalnih točaka koje nisu u interakciji jedna s drugom. Objasnimo ovu definiciju detaljnije.
Prvo, govorimo o materijalnim točkama kao objektima koji čine idealni plin. To znači da njegove molekule i atomi nemaju veličinu, ali imaju određenu masu. Podebljano jeaproksimacija se može napraviti uzimajući u obzir činjenicu da je u svim stvarnim plinovima pri niskim tlakovima i visokim temperaturama udaljenost između molekula mnogo veća od njihovih linearnih dimenzija.
Drugo, molekule u idealnom plinu ne bi trebale komunicirati jedna s drugom. U stvarnosti, takve interakcije uvijek postoje. Dakle, čak i atomi plemenitih plinova doživljavaju dipol-dipolnu privlačnost. Drugim riječima, prisutne su van der Waalsove interakcije. Međutim, u usporedbi s kinetičkom energijom rotacije i translacijskog kretanja molekula, te su interakcije toliko male da ne utječu na svojstva plinova. Stoga se ne mogu uzeti u obzir pri rješavanju praktičnih problema.
Važno je napomenuti da se svi plinovi u kojima je niska gustoća i visoka temperatura ne mogu smatrati idealnim. Osim van der Waalsovih interakcija, postoje i druge, jače vrste veza, na primjer, vodikove veze između H2O molekula, koje dovode do grubog kršenja uvjeta idealnosti plina. Iz tog razloga, vodena para nije idealan plin, ali zrak jest.
Fizički model idealnog plina
Ovaj model se može predstaviti na sljedeći način: pretpostavimo da plinski sustav sadrži N čestica. To mogu biti atomi i molekule raznih kemikalija i elemenata. Broj N čestica je velik, pa se za njegovo opisivanje obično koristi jedinica "mol" (1 mol odgovara Avogadrovom broju). Svi se kreću u nekom volumenu V. Kretanja česticasu kaotični i neovisni jedno o drugom. Svaki od njih ima određenu brzinu v i kreće se ravnom stazom.
Teoretski, vjerojatnost sudara između čestica je gotovo nula, budući da je njihova veličina mala u usporedbi s udaljenostima između čestica. Međutim, ako dođe do takvog sudara, onda je apsolutno elastičan. U potonjem slučaju, ukupni zamah čestica i njihova kinetička energija su očuvani.
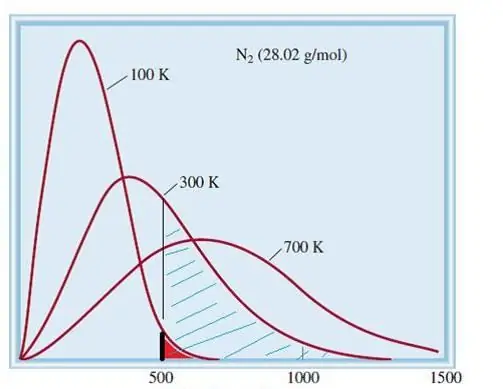
Razmatrani model idealnih plinova je klasičan sustav s ogromnim brojem elemenata. Stoga se brzina i energija čestica u njemu pokoravaju statističkoj raspodjeli Maxwell-Boltzmanna. Neke čestice imaju male brzine, dok druge imaju velike brzine. U ovom slučaju postoji određena uska granica brzine u kojoj se nalaze najvjerojatnije vrijednosti ove količine. Raspodjela brzina molekula dušika je shematski prikazana ispod.
Kinetička teorija plinova
Model idealnih plinova opisan gore na jedinstven način određuje svojstva plinova. Ovaj model je prvi predložio Daniel Bernoulli 1738.

Naknadno su ga do sadašnjeg stanja razvili August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski i drugi znanstvenici.
Kinetička teorija fluidnih tvari, na temelju koje se gradi model idealnog plina, objašnjava dva važna makroskopska svojstva sustava na temelju njegovog mikroskopskog ponašanja:
- Tlak u plinovima rezultat je sudara čestica sa stijenkama posude.
- Temperatura u sustavu je rezultat manifestacije stalnog kretanja molekula i atoma.
Proširimo oba zaključka kinetičke teorije.
Tlak plina
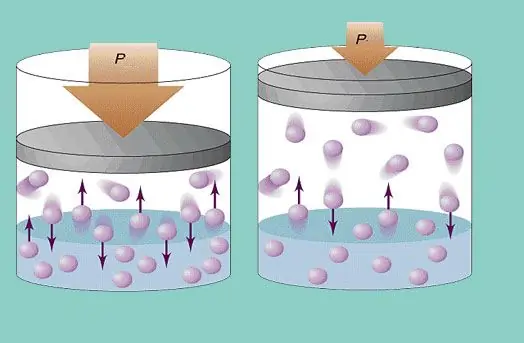
Model idealnog plina pretpostavlja stalno kaotično kretanje čestica u sustavu i njihov stalni sudar sa stijenkama posude. Svaki takav sudar smatra se apsolutno elastičnim. Masa čestica je mala (≈10-27-10-25 kg). Stoga ne može stvoriti veliki pritisak u sudaru. Ipak, broj čestica, a time i broj sudara, je ogroman (≈1023). Osim toga, srednja kvadratna brzina elemenata je nekoliko stotina metara u sekundi na sobnoj temperaturi. Sve to dovodi do stvaranja značajnog pritiska na stijenke posude. Može se izračunati pomoću sljedeće formule:
P=Nmvcp2 / (3V), gdje je vcp srednja kvadratna brzina, m je masa čestice.
Apsolutna temperatura
Prema modelu idealnog plina, temperatura je jedinstveno određena prosječnom kinetičkom energijom molekule ili atoma u sustavu koji se proučava. Možete napisati sljedeći izraz koji povezuje kinetičku energiju i apsolutnu temperaturu za idealni plin:
mvcp2 / 2=3 / 2kB T.
Ovdje je kB Boltzmannova konstanta. Iz ove jednakosti dobivamo:
T=m vcp2 / (3kB).
Univerzalna jednadžba stanja
Ako kombiniramo gornje izraze za apsolutni tlak P i apsolutnu temperaturu T, možemo napisati sljedeću jednakost:
PV=nRT.
Ovdje je n količina tvari u molovima, R je plinska konstanta koju je uveo D. I. Mendeljejev. Ovaj izraz je najvažnija jednadžba u teoriji idealnih plinova, jer kombinira tri termodinamička parametra (V, P, T) i ne ovisi o kemijskim karakteristikama plinskog sustava.

Univerzalna jednadžba prvi je eksperimentalno izvedena od strane francuskog fizičara Emilea Clapeyrona u 19. stoljeću, a zatim je doveo u njen moderni oblik od strane ruskog kemičara Mendeljejeva, zbog čega trenutno nosi imena ovih znanstvenika.






