Fizika: formula otpornosti i Ohmov zakon

2024 Autor: Angel Austin | [email protected]. Zadnja promjena: 2024-01-02 17:48

Ohmov zakon je osnovni zakon električnih krugova. Ujedno nam omogućuje da objasnimo mnoge prirodne pojave. Na primjer, može se razumjeti zašto struja ne "pobijedi" ptice koje sjede na žicama. Za fiziku je Ohmov zakon izuzetno značajan. Bez njegovog znanja bilo bi nemoguće stvoriti stabilne električne krugove ili uopće ne bi bilo elektronike.

Zavisnost I=I(U) i njezina vrijednost

Povijest otkrića otpornosti materijala izravno je povezana sa strujno-naponskom karakteristikom. Što je? Uzmimo krug s konstantnom električnom strujom i razmotrimo bilo koji od njegovih elemenata: svjetiljku, plinsku cijev, metalni vodič, tikvicu s elektrolitom, itd.

Promjenom napona U (često se naziva V) koji se dovodi na dotični element, pratit ćemo promjenu jačine struje (I) koja prolazi kroz njega. Kao rezultat toga, dobit ćemo ovisnost oblika I \u003d I (U), koji se naziva "naponska karakteristika elementa" i izravan je pokazatelj njegovogelektrična svojstva.

V/A karakteristika može izgledati drugačije za različite elemente. Njegov najjednostavniji oblik dobiva se razmatranjem metalnog vodiča, što je napravio Georg Ohm (1789. - 1854.).

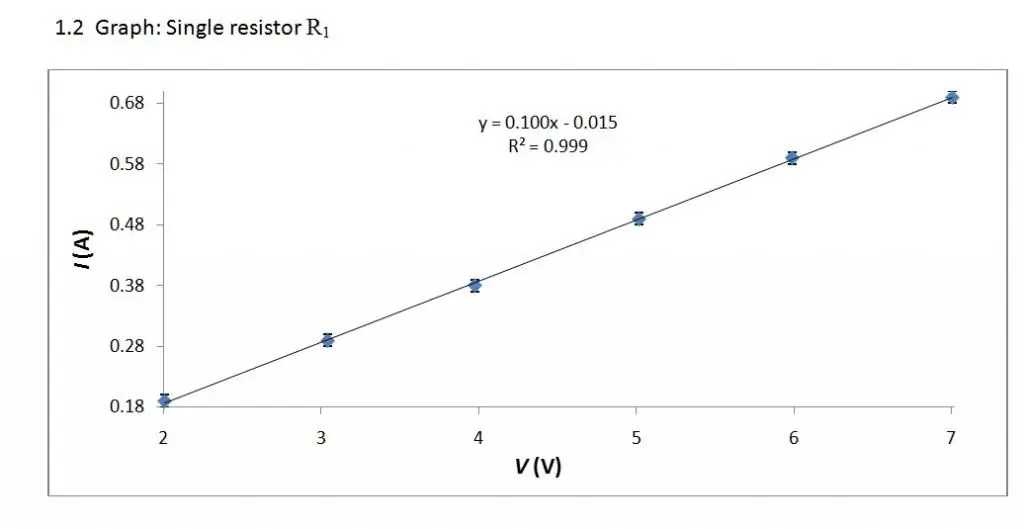
Volt-amperska karakteristika je linearni odnos. Stoga je njegov graf ravna linija.

Zakon u najjednostavnijem obliku

Ohmovo istraživanje strujno-naponskih karakteristika vodiča pokazalo je da je jačina struje unutar metalnog vodiča proporcionalna razlici potencijala na njegovim krajevima (I ~ U) i obrnuto proporcionalna određenom koeficijentu, odnosno I ~ 1/R. Ovaj koeficijent postao je poznat kao "otpor provodnika", a jedinica mjerenja električnog otpora bila je Ohm ili V/A.

Još jednu stvar za napomenuti. Ohmov zakon se često koristi za izračunavanje otpora u krugovima.

formulacija zakona

Ohmov zakon kaže da je jačina struje (I) jednog dijela kruga proporcionalna naponu u ovom dijelu i obrnuto proporcionalna njegovom otporu.

Treba napomenuti da u ovom obliku zakon vrijedi samo za homogeni dio lanca. Homogen je onaj dio električnog kruga koji ne sadrži izvor struje. Kako koristiti Ohmov zakon u nehomogenom krugu bit će razmotreno u nastavku.

Kasnije je eksperimentalno utvrđeno da zakon ostaje na snazi za rješenjaelektroliti u električnom krugu.

Fizičko značenje otpora

Otpor je svojstvo materijala, tvari ili medija koje sprječava prolaz električne struje. Kvantitativno, otpor od 1 ohma znači da u vodiču s naponom od 1 V na krajevima može proći električna struja od 1 A.

Električna otpornost

Eksperimentalno je utvrđeno da otpor električne struje vodiča ovisi o njegovim dimenzijama: duljini, širini, visini. A također i na njegov oblik (sfera, cilindar) i materijal od kojeg je izrađen. Dakle, formula za otpornost, na primjer, homogenog cilindričnog vodiča bit će: R \u003d pl / S.

Ako u ovoj formuli stavimo s=1 m2 i l=1 m, tada će R biti brojčano jednak p. Odavde se izračunava jedinica mjere za koeficijent otpornosti vodiča u SI - ovo je Ohmm.

U formuli otpora, p je koeficijent otpora određen kemijskim svojstvima materijala od kojeg je vodič napravljen.

Da bismo razmotrili diferencijalni oblik Ohmovog zakona, moramo razmotriti još nekoliko koncepata.

Trenutačna gustoća

Kao što znate, električna struja je strogo uređeno kretanje bilo koje nabijene čestice. Na primjer, u metalima su nosioci struje elektroni, a u vodljivim plinovima ioni.

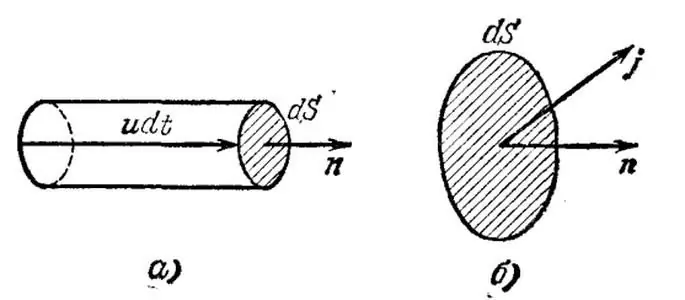
Uzmite trivijalni slučaj kada su svi trenutni operaterihomogen - metalni vodič. Mentalno izdvojimo beskonačno mali volumen u ovom vodiču i označimo s u prosječnu (pokretnu, uređenu) brzinu elektrona u zadanom volumenu. Nadalje, neka n označava koncentraciju nositelja struje po jedinici volumena.

Sada nacrtajmo beskonačno malu površinu dS okomitu na vektor u i konstruirajmo duž brzine beskonačno mali cilindar visine udt, gdje dt označava vrijeme tijekom kojeg će proći svi trenutni nosioci brzine sadržani u razmatranom volumenu kroz područje dS.

U ovom slučaju, naboj jednak q=neudSdt prenijet će elektroni kroz područje, gdje je e naboj elektrona. Dakle, gustoća električne struje je vektor j=neu, koji označava količinu naboja prenesenog u jedinici vremena kroz jediničnu površinu.

Jedna od prednosti diferencijalne definicije Ohmovog zakona je da često možete proći bez izračunavanja otpora.

Punjenje struje. Jačina električnog polja

Jačina polja zajedno s električnim nabojem temeljni je parametar u teoriji elektriciteta. U isto vrijeme, kvantitativna predodžba o njima može se dobiti iz jednostavnih eksperimenata dostupnih školarcima.

Radi jednostavnosti, razmotrit ćemo elektrostatičko polje. Ovo je električno polje koje se ne mijenja s vremenom. Takvo polje može se stvoriti stacionarnim električnim nabojem.

Također, potrebna je probna naplata za naše potrebe. U svom kapacitetu koristit ćemo nabijeno tijelo – toliko malo da nije sposobno uzrokovatibilo kakve perturbacije (preraspodjela naboja) u okolnim objektima.

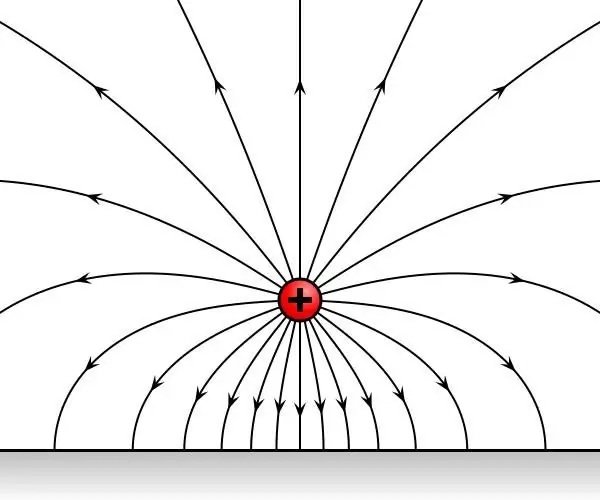
Razmotrimo redom dva uzeta testna naboja, sukcesivno postavljena u jednu točku u prostoru, koja je pod utjecajem elektrostatičkog polja. Ispada da će optužbe biti podvrgnute vremenski nepromjenjivom utjecaju s njegove strane. Neka F₁ i F_{2 budu sile koje djeluju na naboje.}

Kao rezultat generalizacije eksperimentalnih podataka, ustanovljeno je da su sile F₁ i F₂ usmjerene ili u jednu ili u suprotnim smjerovima, a njihov omjer F₁/F₂ je neovisan o točki u prostoru gdje su naizmjenično postavljeni ispitni naboji. Stoga je omjer F₁/F_{2 karakteristika samih naboja i ne ovisi o polju.}

Otkriće ove činjenice omogućilo je karakterizaciju elektrizacije tijela i kasnije je nazvano električni naboj. Dakle, po definiciji, ispada q₁/q₂=F₁/F ₂ , gdje je q₁ i q₂ - iznos troškova postavljenih na jednoj točki polja, i F 1 _{i F}2 _{- sile koje djeluju na naboje sa strane polja.}

Iz takvih razmatranja eksperimentalno su utvrđene veličine naboja različitih čestica. Uvjetnim postavljanjem jednog od testnih naboja jednakim jedan u omjeru, možete izračunati vrijednost drugog naboja mjerenjem omjera F₁/F_2.

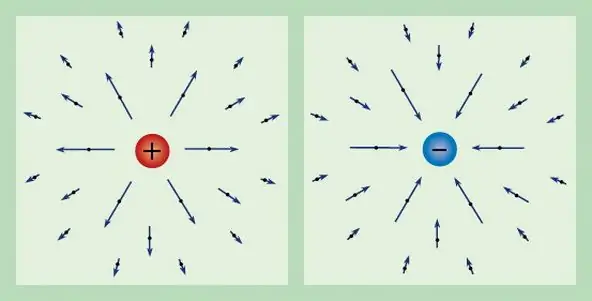
Svako električno polje može se okarakterizirati kroz poznati naboj. Dakle, sila koja djeluje na jedinični ispitni naboj u mirovanju naziva se jakost električnog polja i označava se s E. Iz definicije naboja dobivamo da vektor jakosti ima sljedeći oblik: E=F/q.

Veza vektora j i E. Drugi oblik Ohmovog zakona

U homogenom vodiču, uređeno gibanje nabijenih čestica odvijat će se u smjeru vektora E. To znači da će vektori j i E biti suusmjereni. Kao i pri određivanju gustoće struje, odabiremo beskonačno mali cilindrični volumen u vodiču. Tada će kroz presjek ovog cilindra proći struja jednaka jdS, a napon primijenjen na cilindar bit će jednak Edl. Formula za otpornost cilindra je također poznata.

Onda, zapisivanjem formule za jačinu struje na dva načina, dobivamo: j=E/p, gdje se vrijednost 1/p naziva električna vodljivost i inverzna je električnom otporu. Obično se označava σ (sigma) ili λ (lambda). Jedinica vodljivosti je Sm/m, gdje je Sm Siemens. Jedinica inverzna od Ohma.

Dakle, možemo odgovoriti na gore postavljeno pitanje o Ohmovom zakonu za nehomogeni krug. U tom slučaju na nosioce struje djelovat će sila iz elektrostatičkog polja, koju karakterizira intenzitet E₁, i druge sile koje na njih djeluju iz drugog izvora struje, a koje se mogu označeno E ₂. Tada se primjenjuje Ohmov zakonnehomogeni dio lanca će izgledati ovako: j=λ(E₁ + E_2).

Više o vodljivosti i otpornosti

Sposobnost vodiča da provodi električnu struju karakterizira njegova otpornost, koja se može pronaći pomoću formule otpornosti, ili vodljivosti, izračunate kao recipročna vrijednost vodljivosti. Vrijednost ovih parametara određena je i kemijskim svojstvima materijala vodiča i vanjskim uvjetima. Konkretno, temperatura okoline.

Za većinu metala otpornost pri normalnoj temperaturi je proporcionalna njoj, odnosno p ~ T. Međutim, odstupanja se opažaju pri niskim temperaturama. Za veliki broj metala i legura na temperaturama blizu 0°K, proračun otpora pokazao je nulte vrijednosti. Taj se fenomen naziva supravodljivost. Na primjer, ovo svojstvo imaju živa, kositar, olovo, aluminij itd. Svaki metal ima svoju kritičnu temperaturu T_{k, na kojoj se opaža fenomen supravodljivosti.}

Također imajte na umu da se definicija otpornosti cilindra može generalizirati na žice izrađene od istog materijala. U ovom slučaju, površina poprečnog presjeka iz formule otpora bit će jednaka poprečnom presjeku žice, a l - njezinoj duljini.