Proučavanje procesa koji se odvijaju u statističkim sustavima komplicirano je minimalnom veličinom čestica i njihovim ogromnim brojem. Praktički je nemoguće razmotriti svaku česticu zasebno, stoga se uvode statističke veličine: prosječna brzina čestica, njihova koncentracija, masa čestica. Formula koja karakterizira stanje sustava, uzimajući u obzir mikroskopske parametre, zove se osnovna jednadžba molekularno-kinetičke teorije plinova (MKT).
Malo o prosječnoj brzini čestica
Određivanje brzine čestica prvo je provedeno eksperimentalno. Poznati eksperiment iz školskog kurikuluma, koji je proveo Otto Stern, omogućio je stvaranje ideje o brzinama čestica. Tijekom pokusa proučavano je gibanje atoma srebra u rotirajućim cilindrima: prvo u stacionarnom stanju instalacije, zatim kada je rotirala određenom kutnom brzinom.
Kao rezultat toga, ustanovljeno je da brzina molekula srebra premašuje brzinu zvuka i iznosi 500 m/s. Činjenica je prilično zanimljiva, budući da je čovjeku teško osjetiti takve brzine kretanja čestica u tvarima.
Idealni plin
Nastavite istraživanjeČini se mogućim samo u sustavu čiji se parametri mogu odrediti izravnim mjerenjima pomoću fizičkih instrumenata. Brzina se mjeri brzinomjerom, ali ideja da se brzinomjer pričvrsti na jednu česticu je apsurdna. Samo makroskopski parametar povezan s gibanjem čestica može se izravno mjeriti.
Uzmite u obzir tlak plina. Pritisak na stijenke posude nastaje udarima molekula plina u posudi. Posebnost plinovitog stanja tvari je u dovoljno velikim udaljenostima između čestica i njihovoj maloj međusobnoj interakciji. To vam omogućuje da izravno izmjerite njegov tlak.
Svaki sustav tijela u interakciji karakterizira potencijalna energija i kinetička energija gibanja. Pravi plin je složen sustav. Promjenjivost potencijalne energije ne podliježe sistematizaciji. Problem se može riješiti uvođenjem modela koji nosi karakteristična svojstva plina, odbacujući složenost interakcije.
Idealni plin je stanje tvari u kojem je interakcija čestica zanemariva, potencijalna energija interakcije teži nuli. Samo energija kretanja, koja ovisi o brzini čestica, može se smatrati značajnom.
Idealni tlak plina
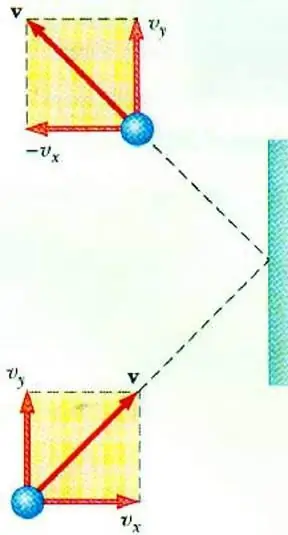
Otkrivanje odnosa između tlaka plina i brzine njegovih čestica omogućuje osnovnu jednadžbu MKT idealnog plina. Čestica koja se kreće u posudi pri udaru o zid prenosi joj impuls čija se vrijednost može odrediti na temelju drugog zakonaNewton:
F∆t=2m0vx
Promjena količine gibanja čestice tijekom elastičnog udara povezana je s promjenom horizontalne komponente njezine brzine. F je sila koja djeluje sa strane čestice na zid za kratko vrijeme t; m0 - masa čestica.
Sve čestice plina sudaraju se s površinom područja S tijekom vremena ∆t, krećući se u smjeru površine brzinom vx i nalaze se u cilindru volumena Sυ x Δt. Pri koncentraciji čestica n, točno polovica molekula kreće se prema zidu, a druga polovica se kreće u suprotnom smjeru.
Razmatrajući sudar svih čestica, možemo napisati Newtonov zakon za silu koja djeluje na površinu:
F∆t=nm0vx2S∆t
Budući da je tlak plina definiran kao omjer sile koja djeluje okomito na površinu i površine potonje, možemo napisati:
p=F: S=nm0vx2
Rezultirajuća relacija kao osnovna jednadžba MKT-a ne može opisati cijeli sustav, budući da se razmatra samo jedan smjer kretanja.
Maxwellova distribucija
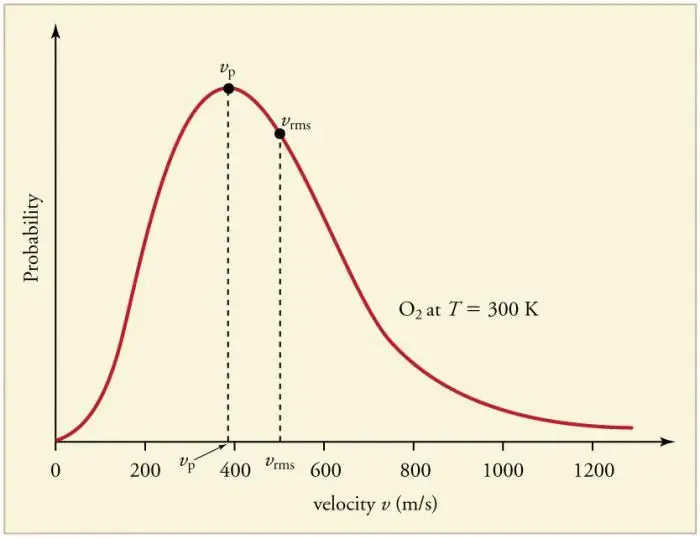
Neprekidni česti sudari čestica plina sa stijenkama i međusobno dovode do uspostavljanja određene statističke raspodjele čestica u smislu brzina (energija). Smjerovi svih vektora brzina pokazuju se jednako vjerojatnim. Ova se raspodjela naziva Maxwellova distribucija. Godine 1860. ovaj obrazac jeizveo J. Maxwell na temelju MKT. Glavni parametri zakona distribucije nazivaju se brzine: vjerojatna, koja odgovara maksimalnoj vrijednosti krivulje, i srednji kvadrat vkv=√‹v2 › - srednji kvadrat brzine čestice.
Povećanje temperature plina odgovara povećanju brzine.
Na osnovu činjenice da su sve brzine jednake, a njihovi moduli imaju istu vrijednost, možemo pretpostaviti:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, od: ‹ vx2›=‹v2›: 3
Osnovna jednadžba MKT-a, uzimajući u obzir prosječnu vrijednost tlaka plina, glasi:
p=nm0‹v2›: 3.
Ovaj odnos je jedinstven po tome što određuje odnos između mikroskopskih parametara: brzine, mase čestica, koncentracije čestica i tlaka plina općenito.
Upotrebom koncepta kinetičke energije čestica, osnovna jednadžba MKT-a može se prepisati drugačije:
p=2nm0‹v2›: 6=2n‹Ek›: 3
Tlak plina proporcionalan je prosječnoj vrijednosti kinetičke energije njegovih čestica.
temperatura
Zanimljivo je da se za konstantnu količinu plina u zatvorenoj posudi može povezati tlak plina i prosječnu vrijednost energije gibanja čestice. U tom slučaju tlak se može mjeriti mjerenjem energiječestice.
Što učiniti? Koja se vrijednost može usporediti s kinetičkom energijom? Pokazalo se da je temperatura takva vrijednost.

Temperatura je mjera toplinskog stanja tvari. Za njegovo mjerenje koristi se termometar, čija je osnova toplinska ekspanzija radne tekućine (alkohol, živa) kada se zagrijava. Skala termometra se stvara eksperimentalno. Obično se na njemu stavljaju oznake koje odgovaraju položaju radnog fluida tijekom nekog fizičkog procesa koji se odvija u konstantnom toplinskom stanju (kipuća voda, otapanje leda). Različiti termometri imaju različite skale. Na primjer, Celzijus, Fahrenheit.

Univerzalna temperaturna skala
Plinski termometri mogu se smatrati zanimljivijim u smislu neovisnosti o svojstvima radnog fluida. Njihova ljestvica ne ovisi o vrsti plina koji se koristi. U takvom uređaju hipotetski se može izdvojiti temperatura pri kojoj tlak plina teži nuli. Izračuni pokazuju da ova vrijednost odgovara -273,15 oC. Temperaturna ljestvica (ljestvica apsolutne temperature ili Kelvinova skala) uvedena je 1848. godine. Za glavnu točku ove ljestvice uzeta je moguća temperatura nultog tlaka plina. Jedinični segment ljestvice jednak je jediničnoj vrijednosti Celzijeve ljestvice. Čini se prikladnijim zapisati osnovnu MKT jednadžbu koristeći temperaturu pri proučavanju plinskih procesa.
Odnos između tlaka i temperature
Empirijski to možete potvrditiproporcionalnost tlaka plina njegovoj temperaturi. Istovremeno je utvrđeno da je tlak izravno proporcionalan koncentraciji čestica:
P=nkT,
gdje je T apsolutna temperatura, k je konstanta jednaka 1,38•10-23J/K.
Osnovna vrijednost, koja ima konstantnu vrijednost za sve plinove, naziva se Boltzmannova konstanta.
Uspoređujući ovisnost tlaka o temperaturi i osnovnu jednadžbu MKT plinova, možemo napisati:
‹Ek›=3kT: 2
Prosječna vrijednost kinetičke energije kretanja molekula plina proporcionalna je njegovoj temperaturi. To jest, temperatura može poslužiti kao mjera kinetičke energije gibanja čestica.






