Plinovi, sa stajališta termodinamike, opisuju se skupom makroskopskih karakteristika od kojih su glavne temperatura, tlak i volumen. Konstantnost jednog od ovih parametara i promjena u druga dva ukazuje na to da se u plinu događa jedan ili drugi izoproces. Ovaj ćemo članak posvetiti detaljnim odgovorima na pitanja da je ovo izohorni proces, kako se razlikuje od izotermnih i izobaričnih promjena stanja plinskog sustava.
Idealan plin u fizici

Prije nego odgovorite na pitanje da je ovo izohorni proces, trebali biste bolje upoznati pojam idealnog plina. U fizici se podrazumijeva svaki plin u kojem prosječna kinetička energija njegovih sastavnih čestica daleko premašuje potencijalnu energiju njihove interakcije, a udaljenosti između tih čestica su nekoliko redova veličine veće od njihovih linearnih dimenzija. Pod navedenim uvjetima, moguće je, prilikom izvođenjaproračuni ne uzimaju u obzir energiju interakcije između čestica (jednaka je nuli), a također se može pretpostaviti da su čestice materijalne točke određene mase m.
Jedini proces koji se odvija u idealnom plinu je sudar čestica sa stijenkama posude koja sadrži tvar. Ti se sudari manifestiraju u praksi kao postojanje određenog tlaka u plinu P.
U pravilu se svaka plinovita tvar koja se sastoji od relativno kemijski inertnih molekula i koja ima nizak tlak i visoke temperature može smatrati idealnim plinom s dovoljnom točnošću za praktične izračune.
Jednadžba koja opisuje idealni plin
Naravno, govorimo o univerzalnom zakonu Clapeyron-Mendeleeva, koji treba dobro razumjeti da bi se shvatilo da se radi o izohoričnom procesu. Dakle, univerzalna jednadžba stanja ima sljedeći oblik:
PV=nRT.
To jest, umnožak tlaka P i volumena plina V jednak je umnošku apsolutne temperature T i količine tvari u molovima n, gdje je R faktor proporcionalnosti. Samu jednadžbu prvi je napisao Emile Clapeyron 1834. godine, a 70-ih godina 19. stoljeća D. Mendelejev je u njoj zamijenio skup konstantnih vrijednosti jedne univerzalne plinske konstante R (8,314 J/(molK).)).
U skladu s Clapeyron-Mendelejevom jednadžbom, u zatvorenom sustavu broj čestica plina ostaje konstantan, tako da postoje samo tri makroskopska parametra koja se mogu mijenjati (T, Pi V). Posljednja činjenica je u temelju razumijevanja različitih izoprocesa o kojima će se raspravljati u nastavku.
Što je izohorični proces?
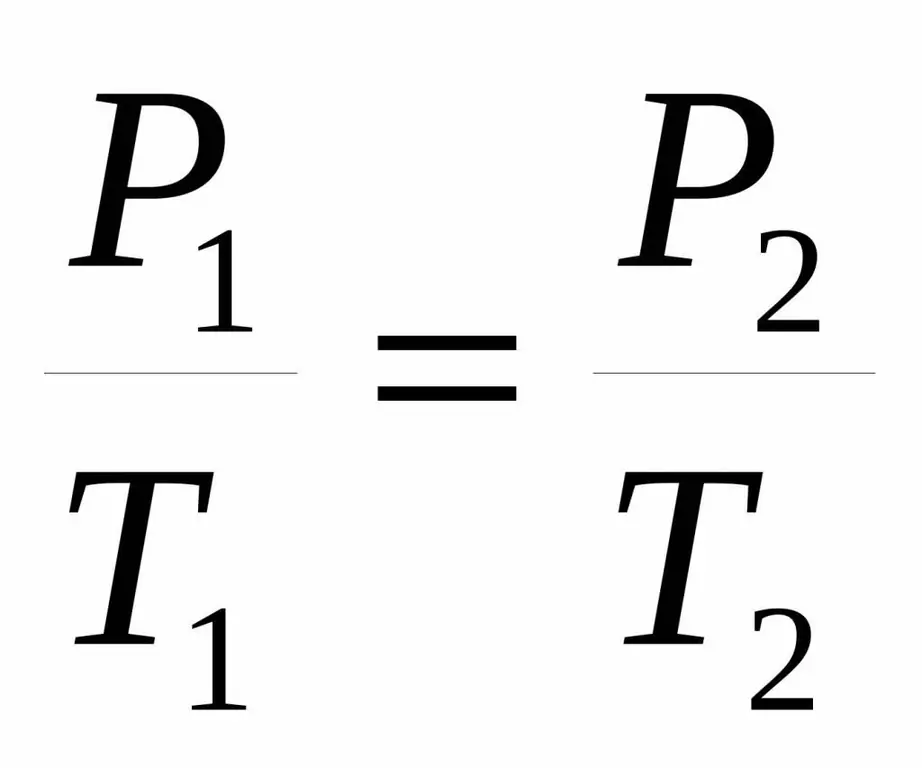
Ovaj proces razumijeva se kao apsolutno svaka promjena stanja sustava u kojoj je sačuvan njegov volumen.
Ako se okrenemo univerzalnoj jednadžbi stanja, možemo reći da se u izohoričnom procesu mijenjaju samo tlak i apsolutna temperatura u plinu. Da bismo točno razumjeli kako se termodinamički parametri mijenjaju, pišemo odgovarajući matematički izraz:
P / T=konst.
Ponekad se ova jednakost daje u malo drugačijem obliku:
P1 / T1=P2 / T 2.
Obje jednakosti nazivaju se Charlesovim zakonom po imenu francuskog znanstvenika koji je krajem 18. stoljeća eksperimentalno dobio zapaženu ovisnost.

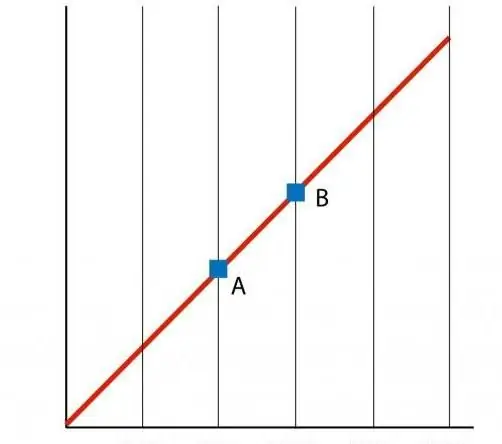
Ako izgradimo graf funkcije P(T), tada dobivamo pravocrtnu ovisnost, koja se naziva izohora. Bilo koja izokora (za sve vrijednosti n i V) je ravna linija.
Energijski opis procesa
Kao što je navedeno, izohorični proces je promjena stanja sustava koja se odvija u zatvorenom, ali ne izoliranom sustavu. Govorimo o mogućnosti izmjene topline između plina i okoline. Općenito, svaka opskrba toplinom Q sustavu dovodi do dva rezultata:
- mjenja unutarnju energiju U;
- plinradi A, širi se ili skuplja.
Posljednji zaključak je napisan matematički na sljedeći način:
Q=U + A.
Izohorični proces idealnog plina, po svojoj definiciji, ne podrazumijeva rad koji obavlja plin, budući da njegov volumen ostaje nepromijenjen. To znači da sva toplina dovedena u sustav ide za povećanje njegove unutarnje energije:
Q=U.
Ako u ovaj izraz zamijenimo eksplicitnu formulu za unutarnju energiju, tada se toplina izohoričkog procesa može predstaviti kao:
Q=z / 2nRT.
Ovdje je z broj stupnjeva slobode, koji je određen poliatomskom prirodom molekula koje čine plin. Za jednoatomski plin, z=3, za dvoatomski plin - 5, a za troatomski i više - 6. Ovdje pod stupnjevima slobode podrazumijevamo translacijske i rotacijske stupnjeve.
Uporedimo li učinkovitost zagrijavanja plinskog sustava u izohoričnim i izobaričnim procesima, tada ćemo u prvom slučaju dobiti maksimalnu učinkovitost, budući da se tijekom izobarične promjene stanja sustava plin širi, a dio uložene topline troši se na rad.
Izobarični proces
Gore smo detaljno opisali da je ovo izohorični proces. Recimo sada nekoliko riječi o drugim izoprocesima. Počnimo s izobarskim. Na temelju naziva shvaća se kao prijelaz sustava između stanja pri konstantnom pritisku. Ovaj proces opisuje Gay-Lussac zakon na sljedeći način:
V / T=konst.
Kao i kod izohore, V(T) izobara također predstavlja ravnu liniju na grafu.
Zabilo kojeg izobarnog procesa, prikladno je izračunati rad plina, budući da je jednak umnošku konstantnog tlaka i promjene volumena.
Izotermički proces
Ovo je proces u kojem temperatura sustava ostaje konstantna. Opisuje ga Boyle-Mariotteov zakon za idealni plin. Zanimljivo je napomenuti da je ovo prvi eksperimentalno otkriven plinski zakon (druga polovica 17. stoljeća). Njegov matematički zapis izgleda ovako:
PV=konst.
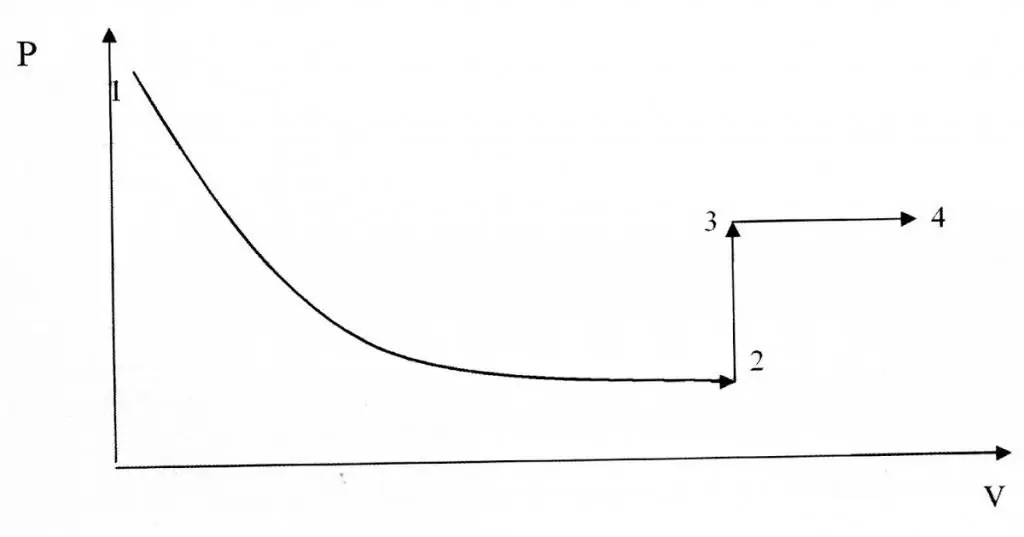
Izohorični i izotermički procesi razlikuju se u smislu njihovog grafičkog prikaza, budući da je funkcija P(V) hiperbolički, a ne linearni odnos.
Primjer rješavanja problema
Objedinimo teorijske informacije navedene u članku njihovom primjenom za rješavanje praktičnog problema. Poznato je da je čisti plinoviti dušik bio u cilindru pri tlaku od 1 atmosfere i temperaturi od 25 °C. Nakon što je plinski cilindar zagrijan i izmjeren tlak u njemu, pokazalo se da iznosi 1,5 atmosfere. Kolika je temperatura plina u cilindru nakon zagrijavanja? Za koliko se promijenila unutarnja energija plina ako je u balonu bilo 4 mola dušika.
Za odgovor na prvo pitanje koristimo sljedeći izraz:
P1 / T1=P2 / T 2.
Odakle dobivamo:
T2=P2 / P1 T 1.
U ovom izrazu tlak se može zamijeniti proizvoljnim jedinicamamjerenja, budući da se smanjuju, a temperatura je samo u kelvinima. Uz to, dobivamo:
T2=1,5 /1298,15=447,224 K.
Izračunata temperatura u stupnjevima Celzijusa je 174 °C.
Budući da je molekula dušika dvoatomska, promjena njezine unutarnje energije tijekom zagrijavanja može se odrediti na sljedeći način:
ΔU=5 / 2nRΔT.
Zamjenom poznatih vrijednosti u ovaj izraz, dobit ćemo odgovor na drugo pitanje problema: ΔU=+12,4 kJ.






