U termodinamici, kada se proučavaju prijelazi iz početnog u konačno stanje sustava, važno je poznavati toplinski učinak procesa. Koncept toplinskog kapaciteta usko je povezan s ovim efektom. U ovom članku razmotrit ćemo pitanje što se podrazumijeva pod izohoričnim toplinskim kapacitetom plina.
Idealni plin
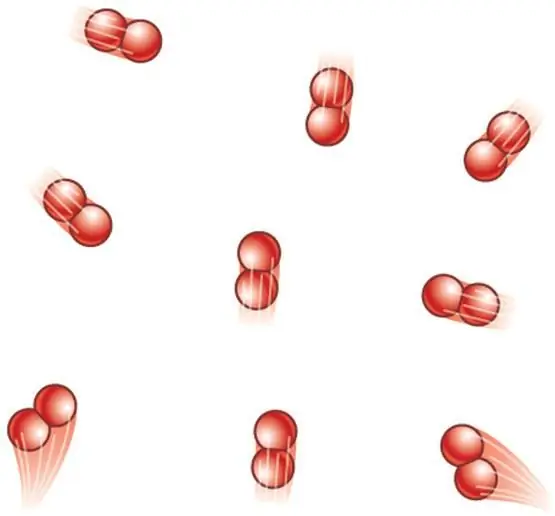
Idealni plin je plin čije se čestice smatraju materijalnim točkama, odnosno nemaju dimenzije, ali imaju masu i u kojem se sva unutarnja energija sastoji isključivo od kinetičke energije kretanja molekula i atomi.
Bilo koji pravi plin u idealnom slučaju nikada neće zadovoljiti opisani model, budući da njegove čestice još uvijek imaju neke linearne dimenzije i međusobno djeluju koristeći slabe van der Waalsove veze ili kemijske veze drugog tipa. Međutim, pri niskim tlakovima i visokim temperaturama udaljenosti između molekula su velike, a njihova kinetička energija premašuje potencijalnu za desetke puta. Sve to omogućuje primjenu s visokim stupnjem točnosti idealnog modela za stvarne plinove.
Unutarnja energija plina
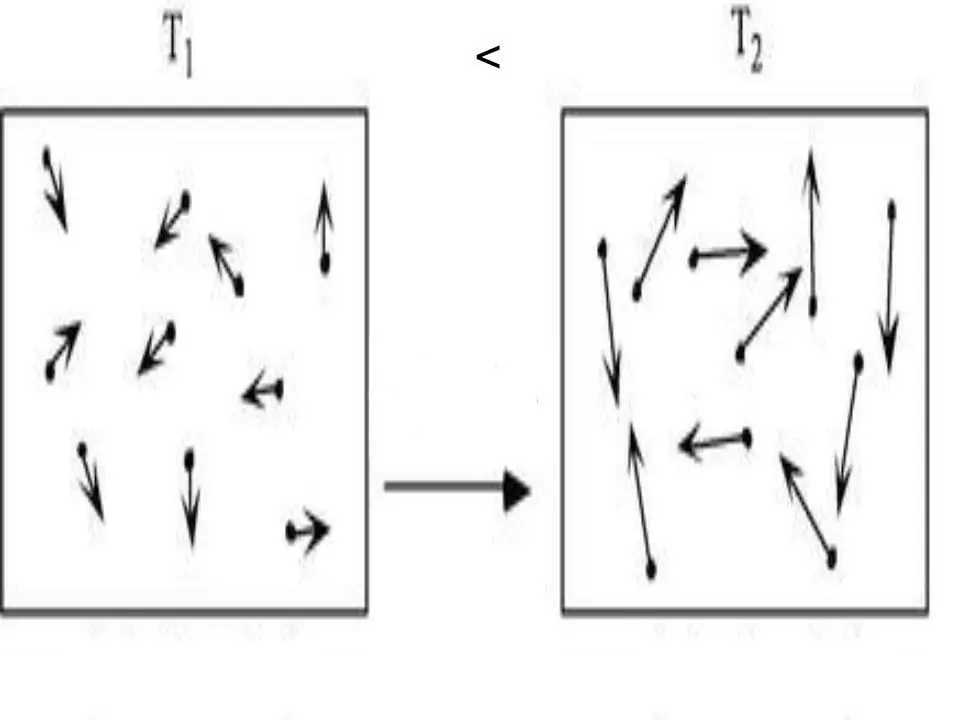
Unutarnja energija bilo kojeg sustava je fizička karakteristika, koja je jednaka zbroju potencijalne i kinetičke energije. Budući da se potencijalna energija može zanemariti u idealnim plinovima, za njih možemo napisati jednakost:
U=Ek.
Gdje je Ek energija kinetičkog sustava. Koristeći molekularnu kinetičku teoriju i primjenom univerzalne Clapeyron-Mendelejevove jednadžbe stanja, nije teško dobiti izraz za U. Dolje je napisano:
U=z/2nRT.
Ovdje su T, R i n apsolutna temperatura, plinska konstanta i količina tvari, respektivno. Z-vrijednost je cijeli broj koji označava broj stupnjeva slobode koje ima molekula plina.
Izobarični i izohorni toplinski kapacitet
U fizici, toplinski kapacitet je količina topline koja se mora predati sustavu koji se proučava kako bi se zagrijao za jedan kelvin. Vrijedi i obrnuta definicija, odnosno toplinski kapacitet je količina topline koju sustav oslobađa kada se ohladi za jedan kelvin.
Najlakši način za sustav je odrediti izohorični toplinski kapacitet. Podrazumijeva se kao toplinski kapacitet pri konstantnom volumenu. Budući da sustav ne obavlja rad u takvim uvjetima, sva energija se troši na povećanje unutarnjih energetskih rezervi. Označimo izohorični toplinski kapacitet simbolom CV, tada možemo napisati:
dU=CVdT.
To jest, promjena unutarnje energijesustav je izravno proporcionalan promjeni njegove temperature. Ako ovaj izraz usporedimo s jednakošću napisanom u prethodnom odlomku, dolazimo do formule za CV u idealnom plinu:
SV=z/2nR.
Ovu vrijednost je nezgodno koristiti u praksi, jer ovisi o količini tvari u sustavu. Stoga je uveden pojam specifičnog izohornog toplinskog kapaciteta, odnosno vrijednosti koja se računa ili na 1 mol plina ili na 1 kg. Označimo prvu vrijednost simbolom CV, drugu - simbolom CV m. Za njih možete napisati sljedeće formule:
CV=z/2R;
CVm=z/2R/M.
Ovdje je M molarna masa.
Izobarični je toplinski kapacitet uz održavanje konstantnog tlaka u sustavu. Primjer takvog procesa je širenje plina u cilindru ispod klipa kada se zagrijava. Za razliku od izohornog procesa, tijekom izobarnog procesa, toplina dovedena u sustav troši se na povećanje unutarnje energije i obavljanje mehaničkog rada, odnosno:
H=dU + PdV.
Entalpija izobarnog procesa umnožak je izobarnog toplinskog kapaciteta i promjene temperature u sustavu, odnosno:
H=CPdT.
Ako uzmemo u obzir ekspanziju pri konstantnom tlaku od 1 mol plina, tada će prvi zakon termodinamike biti napisan kao:
CPdT=CV dT + RdT.
Posljednji član dobiva se iz jednadžbeClapeyron-Mendeljejev. Iz ove jednakosti slijedi odnos između izobarnog i izohornog toplinskog kapaciteta:
CP=CV + R.
Za idealni plin, specifični molarni toplinski kapacitet pri konstantnom tlaku uvijek je veći od odgovarajuće izohorične karakteristike za R=8, 314 J/(molK).
Stupanji slobode molekula i toplinski kapacitet
Napišimo ponovo formulu za specifični molarni izohorični toplinski kapacitet:
CV=z/2R.
U slučaju jednoatomskog plina, vrijednost z=3, budući da se atomi u svemiru mogu kretati samo u tri neovisna smjera.
Ako govorimo o plinu koji se sastoji od dvoatomskih molekula, na primjer, kisik O2 ili vodik H2, tada, osim translacijskog gibanja, ove molekule još uvijek mogu rotirati oko dvije međusobno okomite osi, odnosno z će biti jednako 5.
Za složenije molekule, koristite z=6. za određivanje CV






